数学-贝蒂定理

发表于 更新于 分类于
本文字数： 277 阅读时长 ≈ 1 分钟

贝蒂定理（Betti theorem），以意大利数学家恩里科·贝蒂命名

定理内容

若两个正无理数a,b满足

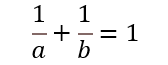
那么对于两个集合A，B

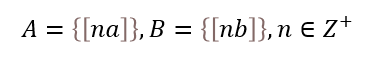
有以下结论

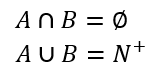
证明

I. 任一个整数至多在集合A或B中出现一次

由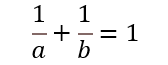且a,b为正可得a,b均大于1，所以[na],[nb]跨度大于1，故向下取整不会有重复元素

II. A∩B为空集

反证法：设存在整数k使得

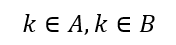
则有

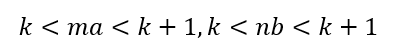
即

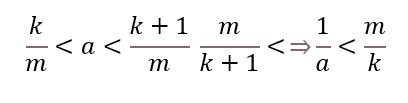
同理

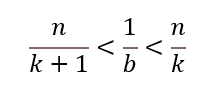
两式相加

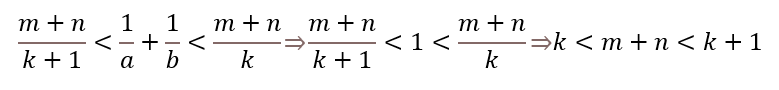
显然，推出结论与m,n为整数矛盾，证毕

III. N+ = A∪B

相当于已知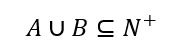

求证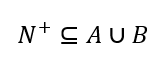

同样采取反证法，设整数k满足

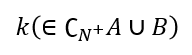
必然存在整数m,n使得

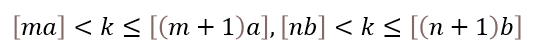
化简得

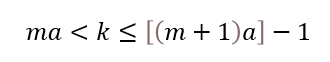
由a为无理数

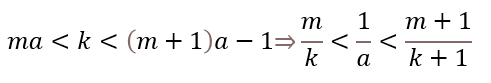
同理

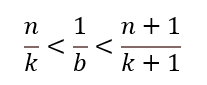
两式相加

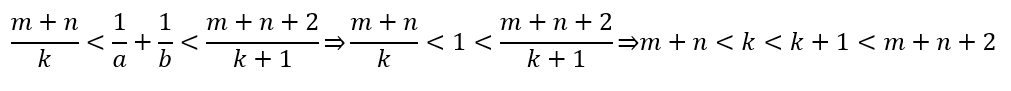
易知m+n与m+n+2间只能有一个整数，结论与假设矛盾，所以不存在k，证毕